MAS 864
Bouncing
ball in java
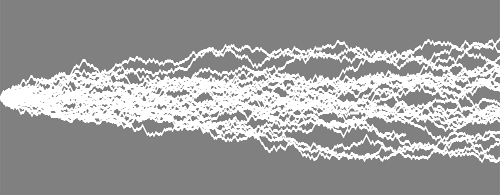
The ball is released at a variable height and bounces with 0.95 of its
speed from the bounding box enclosures.
As its speed in the y direction approaches 0 the simulation blows up and
the ball goes in uncontrolled spin of the screen
I tried to controll this effect in the simulation but was not successful.

The balls path is drawn as a postscript path and saved as an eps file. The starting position and speeds can be






sig^2 n,i/sig^2gr = sum j (V^2 i,j/w^2 j)
2.650558 +- 0.174769
Chi-squared 99.425986
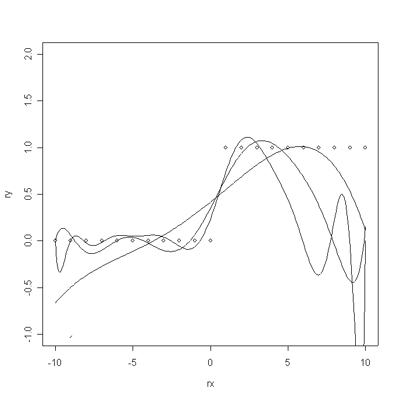
f(x,y) = 0.2(x^2+y^2)-2 *exp(-(x^2)+y^2)) - exp(-(x^2+(y+4)^2))/2)
[1,] 0.4153837165
[2,] 0.1341669391
[3,] 0.0036503410
[4,] -0.0009534706
[5,] -0.0001057958
order 10 coefficients
[1,] 3.505278e-01
[2,] 3.216823e-01
[3,] 2.130687e-02
[4,] -1.792592e-02
[5,] -8.046099e-04
[6,] 4.715427e-04
[7,] 5.854754e-06
[8,] -5.914938e-06
[9,] -2.132643e-09
[10,] 2.678003e-08
order15 coefficients
[1,] 2.356892e-01
[2,] 4.519468e-01
[3,] 1.179799e-01
[4,] -5.303195e-02
[5,] -1.512227e-02
[6,] 3.209537e-03
[7,] 8.446648e-04
[8,] -1.094209e-04
[9,] -2.568237e-05
[10,] 1.978109e-06
[11,] 4.228687e-07
[12,] -1.744958e-08
[13,] -3.487685e-09
[14,] 5.886214e-11
[15,] 1.121760e-11
Inverted
pendulum
An inverted pendulum with a mass of 1kg and a length of 1m is attached
to a fix pivot on a table. It can be controlled by a Force F that acts
at the center of the rod.
(a) first order equations that describe the system
dot_dot_theta = -3/2 F/ml cos theta +3/2 g/l sin theta
Matrix A = [[0,1],[3/2 g/l, 0]] ; Matrix B = [0, 1/M]
matrix C = [B, AB] is of full rank therefore it is controllable problem
(b) F = k1 theta + k2 dot_theta for k1 = 126.67 k2 = 266.67 eigenvalues
are both positive
(c) applet - not finished
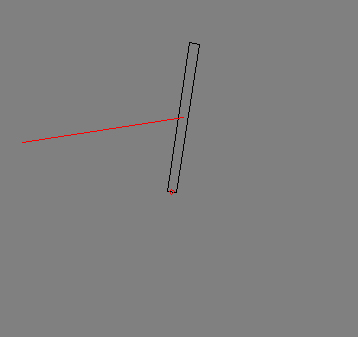
cached version as site was down recently
The modeling
of form rarely takes into account structural performance of the elements
that are being modeled. The proposal is to study how optimization and
structural analysis can be used to influence form making in design process.
Finite elment analysis seems like an approriate method to model material
properties and to give feedback to form making process.
For instance a plank of wood laid onto a curved surface takes a certain
path based on its flexibility and crosssection and based on the curvature
the surface has. At a certain point the plank will not be able to follow
the surface anymore. One possible apporach could be to find distribution
of planks on asurface for optimal coverage based on the mateterial properties.
(depending on level I can achieve in FEM)


java applet

